Hướng dẫn giải bài tập toán lớp 6 tập 1 phép trừ và phép chia chi tiết nhất

Phép trừ và phép chia là những dạng phép tính cơ bản và quan trọng nhất mà ai cũng phải nắm vững. Vì vậy, để giúp các bạn học sinh (đặc biệt là học sinh lớp 6), ôn luyện lại kiến thức và giải quyết được một số bài tập liên quan. Sau đây là hướng dẫn giải một số bài tập toán lớp 6 tập 1 phép trừ và phép chia mà bài viết muốn chia sẻ đến cho bạn.

Ôn tập lý thuyết về phép trừ và phép chia

Trước khi đi đến cách giải các bài tập về phép trừ và phép chia. Thì các bạn cần phải nắm vững những kiến thức về phép tính này. Thực chất, phép trừ và phép chia là các phép tính cơ bản trong toán học mà lớp 6 đã từng học. Vì vậy, để giúp các bạn ôn luyện lại những kiến thức này, hãy cùng bài viết điểm lại một số lý thuyết quan trọng ngay sau đây.

Phép trừ hai số tự nhiên

Cho 2 số tự nhiên gồm a và b. Nếu như có số x làm cho b + x = a, thì ta có được phép trừ là a - b = x. Trong đó, a được xem là số bị trừ, b là số trừ và x chính là hiệu.

Lưu ý: 

• Trong trường hợp b + x = a thì b = a - x và x = a - b.

• Trong trường hợp x = a - b thì b = a - x và b + x = a.

Để có thể thực hiện được dạng phép toán trừ hai số tự nhiên. Điều kiện trong phép tính cần có chính là số bị trừ phải lớn hơn hoặc bằng số trừ.

Phép chia hết và có dư

Phép chia sẽ bao gồm hai dạng chính là chia có dư và chia hết. Cụ thể, các phép tính này sẽ có dạng như sau.

Phép chia hết

Cho 2 số tự nhiên gồm a và b (b ≠ 0). Nếu như có số tự nhiên x khiến cho x.b = a , thì ta sẽ được phép chia hết là x = a : b. Trong đó, a được gọi là số bị chia, b là số chia và x chính là thương.

Phép chia hết. (Ảnh: Monkey)

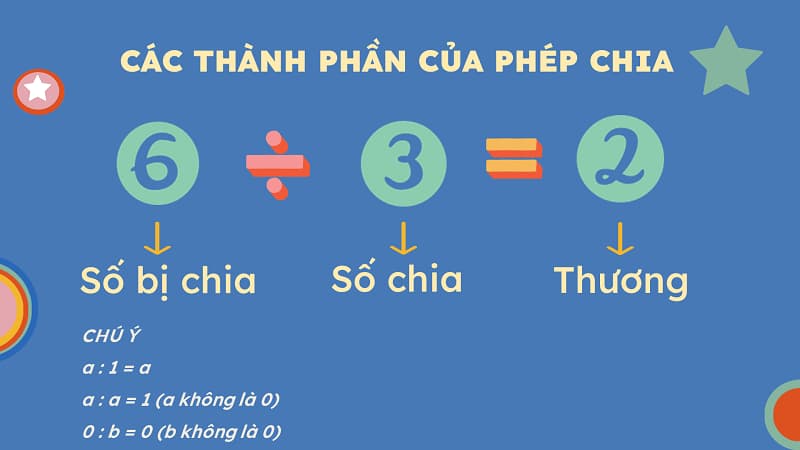
Lưu ý: 

• Nếu b.x = a thì b = a : x (với x ≠ 0) và x = a : b (với b ≠ 0).

• Nếu x = a : b thì b = a : x (với x ≠ 0) và b.x = a.

Phép chia có dư

Cho 2 số tự nhiên gồm a và b (b ≠ 0). Ta sẽ luôn có được 2 con số q và r, sao cho (với a = b.q + r, 0 r < b). Với r ≠ 0, ta nói rằng đây là dạng phép chia có dư với a được xem là số bị chia, b chính là số chia, q là thương và r là số dư. 

Lưu ý: Trong dạng phép tính chia, số chia lúc nào cũng phải khác 0. Nếu như bằng 0, thì dạng phép toán đó không có nghĩa.

Các tính chất của phép trừ và phép chia cần nhớ

Bên cạnh những lý thuyết cơ bản về phép trừ và phép chia. Các bạn cần phải lưu ý đến những tính chất trong các phép tính đó. Điều này nhằm giúp bạn dễ dàng xử lý các bài tập có liên quan.

Tính chất của phép trừ

• Tính chất đầu tiên của phép trừ, chính là khi ta thêm vào một số trừ và số bị trừ (đều có cùng đơn vị). Thì hiệu của phép tính sẽ không bị thay đổi.

Ví dụ: 145 - 67 = (145 + 2) - (67 + 2) = 147 - 69 = 78.

• Tính chất thứ hai của phép trừ, chính là tính chất phân phối giữa phép nhân và phép trừ. Đây là dạng phép tính thường xuất hiện trong đề thi mà bạn cần lưu ý kỹ.

Ví dụ: a.(b - c) = a.b - a.c.Trong đó, với a, b và c là các số tự nhiên (b c).

Tính chất của phép chia

Tính chất đầu tiên của phép chia cũng tương tự như phép trừ. Chính là khi ta nhân số chia và số bị chia với cùng một con số. Thì thương của phép tính đó cũng sẽ không thay đổi.

Ví dụ: 330 : 10 = (330.2) : (10.2) = 660 : 20 = 33.

Bên cạnh đó, phép chia hết còn có một tính chất khá quan trọng. Cụ thể, khi chia một tổng cho một số, ta sẽ có dạng tính chất như sau: (a + b) : c = (a : c) + (b : c). Trong đó, a, b và c là các số tự nhiên (a, b chia hết cho c).

Xem thêm: Hướng dẫn giải bài tập trong toán lớp 6 tập 1 phép cộng và phép nhân chi tiết nhất

Tính chất của phép chia. (Ảnh: Sưu tầm Internet)

Hướng dẫn giải bài tập toán lớp 6 tập 1 phép trừ và phép chia

Để giúp các bạn học sinh ôn lại kiến thức về phép trừ và phép chia tại nhà. Sau đây là các bài tập toán lớp 6 phép trừ số tự nhiên trang 16 cùng lời giải chi tiết. Bạn có thể tham khảo và tự ôn luyện thêm.

Bài 41 trang 23 toán lớp 6 tập 1

Đề: Hà Nội, Huế, Nha Trang và thành phố Hồ Chí Minh đều nằm trên con đường quốc lộ 1 theo thứ tự như trên. Với quãng đường từ Hà Nội đến Huế là 658 km, Hà Nội đến Nha Trang là 1278 km và Hà Nội đến thành phố Hồ Chí Minh là 1710 km. Hãy tính quãng đường từ Huế đến Nha Trang và từ Nha Trang đến thành phố Hồ Chí Minh.

Phương pháp giải:

Toán lớp 6 tập 1 bài 41 trang 22. (Ảnh: Sưu tầm Internet)

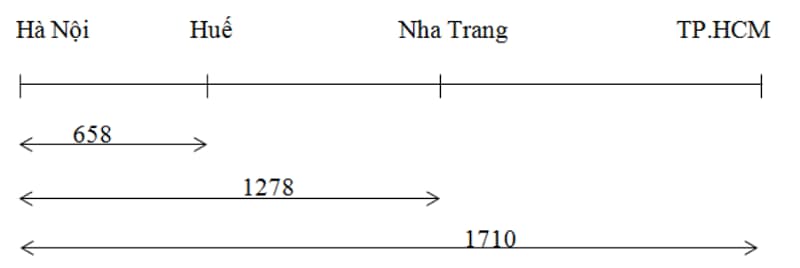
Dựa trên sơ đồ đã vẽ, ta dễ dàng tính được bài toán này như sau:

Quãng đường tính được từ Huế đến Nha Trang là:

1278 - 658 = 620 (km)

Quãng đường tính được từ Nha Trang đến thành phố Hồ Chí Minh là:

1710 - 1278 = 432 (km)

Bài 42 trang 23 toán lớp 6 tập 1

Đề: Cho số liệu về kênh đào Xuy - Ê ở Ai Cập (nối Hồng Hải và Địa Trung Hải) được cho ở bảng 1 và bảng 2.

1. Ở bảng số 1, số liệu vào năm 1955 giảm bớt (hay tăng thêm) bao nhiêu so với năm 1869?

2. Nhờ việc đi qua kênh đào Xuy – Ê, mỗi hành trình của bảng 2 giảm được bao nhiêu km?

Bảng 1

Bảng 2

Phương pháp giải:

1. Ta có số liệu vào năm 1955 so với năm 1869 là:

• Chiều rộng của mặt kênh tăng: 135 - 58 = 77 (m).

• Chiều rộng của đáy kênh tăng: 50 - 22 = 28 (m).

• Độ sâu của con kênh tăng: 13 - 6 = 7 (m).

• Thời gian mà tàu đi qua kênh giảm: 48 - 14 = 34 (giờ).

2. Hành trình khi đi qua kênh đào Xuy – Ê giảm được số km là:

• Hành trình của Luân Đôn – Bom – Bay giảm: 17400 – 10100 = 7300 (km).

• Hành trình của Mác – Xây – Bom – Bay giảm: 16000 – 7400 = 8600 (km).

• Hành trình của Ô – Đét – Xa – Bom – Bay giảm: 19000 – 6800 = 12200 (km).

Bài 43 trang 23 toán lớp 6 tập 1

Đề: Tính khối lượng của quả bí trong hình khi cân ở trạng thái cân bằng:

Bài 43 trang 23 toán lớp 6 tập 1. (Ảnh: Sưu tầm Internet)

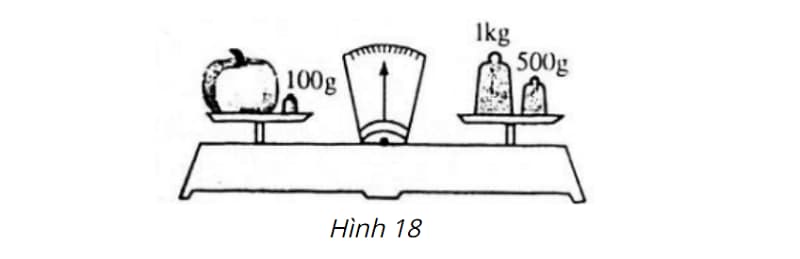
Phương pháp giải:

Ta có, khi cân thăng bằng thì khối lượng ở hai bên cân sẽ bằng nhau, tức là:

Khối lượng bí + 100g = 500g +1kg

Với 1kg = 1000g, ta có khối lượng bí + 100g = 500g + 1000g

Suy ra, khối lượng bí = 500g + 1000g - 100g = 1400g

Vậy: Khối lượng bí = 1400g.

Bài 44 trang 24 toán lớp 6 tập 1

Đề: Tìm x, biết:

1. x : 13 = 41

2. 1428 : x = 14

3. 4x : 17 = 0

4. 7x - 8 = 713

5. 8(x - 3) = 0

6. 0 : x = 0

Phương pháp giải:

1. x : 13 = 41 => x = 4113 = 533

2. 1428 : x = 14 => x = 1428 : 14 = 102

3. 4x : 17 = 0 => 4x = 0.17 = 0 => x = 0

4. 7x - 8 = 713 => 7x = 713 + 8 = 721 => x = 721 : 7 = 103

5. 8(x - 3) = 0 => x - 3 = 0 => x = 3

6. 0 : x = 0 => x thuộc N sao (Bởi vì khi chia 0 với một số tự nhiên bất kỳ khác 0 đều có kết quả bằng 0).

Bài 45 trang 24 toán lớp 6 tập 1

Đề: Điền số phù hợp vào ô trống, sao cho  a = b.q + r, 0 <= r < b.

Phương pháp giải:

Trong dạng phép chia a = b.q + r, 0 <= r < b thì a sẽ là số bị chia, b chính là số chia, q là thương và r là số dư. Vậy, ta sẽ giải theo cách như sau:

• Khi biết trước a và b, ta sẽ tìm thương q và số dư r bằng việc lấy a chia b.

• Khi biết b, q và r trước, thì ta sẽ tìm ra a bằng cách lấy b nhân q cộng r (b.q + r) .

• Khi biết a, q và r trước, thì ta sẽ tìm ra b bằng cách a trừ r sau đó chia cho q ((a - r) : q).

Vậy, ta có được bảng kết quả sau khi thực hiện các phép tính là:

Bài 46 trang 24 toán lớp 6 tập 1

Đề: 

1. Trong phép chia cho 2, thì số dư có thể bằng 1 hoặc bằng 0. Vậy, trong phép chia cho 3, cho 4 và cho 5 thì số dư có thể bằng bao nhiêu?

2. Dạng tổng quát trong phép chia hết cho 2 là 2k, dạng tổng quát trong phép chia cho 2 dư 1 là 2k + 1 (k thuộc N). Hãy viết dạng tổng quát của phép chia hết cho 3, chia 3 dư 1 và chia 3 dư 2.

Phương pháp giải:

1. Trong dạng phép chia số tự nhiên, thì số chia phải lớn hơn số dư a = b.q + r với 0 <= r < b:

• Ở phép chia cho 3, số dư sẽ có thể là: 0, 1 hoặc 2.

• Ở phép chia cho 4, số dư sẽ có thể là: 0, 1, 2 hoặc 3.

• Ở phép chia cho 5, số dư sẽ có thể là: 0, 1, 2, 3 hoặc 4.

2. Ta có dạng tổng quát trong phép chia m dư n chính là m.k + n (k thuộc N).

• Dạng tổng quát của phép chia 3: 3k (k thuộc N).

• Dạng tổng quát của phép chia 3 dư 1: 3k + 1 (k thuộc N).

• Dạng tổng quát của phép chia 3 dư 2: 3k + 2 (k thuộc N).

Hoc10 - Tủ sách số hóa đa năng dành cho học sinh & giáo viên

Bên cạnh những bài tập trong sách giáo khoa, nếu như các bạn học sinh muốn tự luyện thêm về dạng toán này khi ở nhà. Thì tủ sách điện tử Hoc10 chính là một công cụ hữu hiệu mà các bạn không nên bỏ qua.

Hoc10 là tủ sách số hóa được xây dựng bởi các chuyên gia trong lĩnh vực giáo dục. Mang đến cho các bạn học sinh những video minh họa kiến thức, cùng vô vàn dạng bài tập phong phú. Giúp quá trình tự học tại nhà của các bạn đạt được nhiều kết quả tốt. 

Ngoài ra, để giúp các bạn có thể tự ôn tập lại kiến thức cho các kỳ thi. Tại Hoc10 còn có chức năng “Luyện thi” cực kỳ hữu ích dành cho các bạn. Với những dạng bài tập bám sát chương trình giáo dục. Đảm bảo sẽ giúp các bạn làm tốt bài thi của mình khi tham gia ôn luyện tại trang web này.

Hoc10 - Tủ sách số hóa đa năng dành cho học sinh & giáo viên. (Ảnh: Sưu tầm Internet)

Bên cạnh những lợi ích mang lại cho các bạn học sinh, thì Hoc10 còn là một công cụ tâm đắc dành cho giáo viên. Với “góc chia sẻ bài giảng điện tử” được xây dựng bởi đội ngũ giáo viên tài giỏi và giàu kinh nghiệm. Mang đến cho quý thầy cô một kho bài giảng điện tử cực hay và bám sát chương trình dạy. Điều này nhằm mục đích hỗ trợ cho việc giảng dạy của thầy cô được trở nên dễ dàng và thuận tiện hơn. 

Đăng ký tài khoản Miễn Phí để khám phá nhiều điều thú vị về Hoc10 ngay TẠI ĐÂY!

Trên đây là cách giải các bài tập toán lớp 6 tập 1 phép trừ và phép chia mà bài viết đã chia sẻ đến bạn đọc. Với những phương pháp giải chi tiết và siêu đơn giản, hy vọng sẽ giúp ích cho các bạn trong quá trình ôn luyện phép tính này.